One of our “northstar” projects at cgn.ai is indexing the podcast universe — any data of spoken words really. A crucial component of our pipeline is speaker segmentation (or diarization), which involves dividing an audio track into separate speaker tracks and determining who spoke when.
To address this challenge, we have explored various approaches, one of which involves employing a probabilistic model for speaker segmentation. In this approach, we utilize Gen, a general-purpose probabilistic programming system that is integrated within Julia.
The notebook can be found on our public repo at:
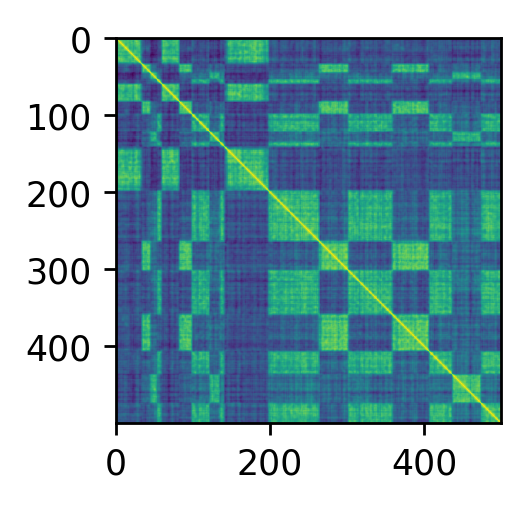
We define a model that generates speaker similarity matrices of a given size. In practice such matrices are constructed by creating voice embeddings $X$ vor a given wav file, and computing their similarity, i.e.
\[D = X X^T.\]To be more precise, we cut the waveform into a collection of (sliding) windows ${w_i}$ which then get mapped to a collection of vector embeddings ${ x_i = f(w_i) }$. Let $w_i$ and $w_j$ be two such audio snippets from a given wav file and let $x_i$ and $x_j$ define their vector embeddings, then the $ij$’th entry is given by
\[d_{i,j} = \langle x_i , x_j \rangle,\]where $\langle x , y \rangle$ denotes the dot-product of $x$ and $y$.
Here is a real world example of such a similarity matrix:
In contrast, here are a few samples from our probabilistic model:
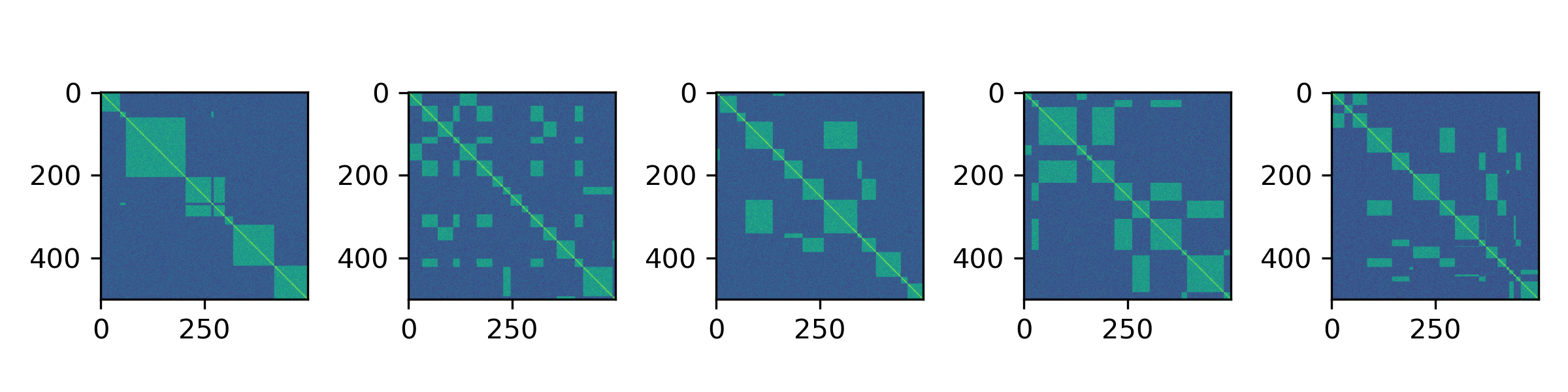
We don’t know how many segments or speakers are present a priori, and to sample from the posterior we turn to Reversible Jump MCMC, an extension to standard MCMC methodology that allows for simulating from a Markov chain whose state is a vector whose dimension is not fixed.
“Reversible jump MCMC”, Peter J. Green and David I. Hastie, Genetics 155.3 (2009).
Inference - Reversible Jump MCMC:
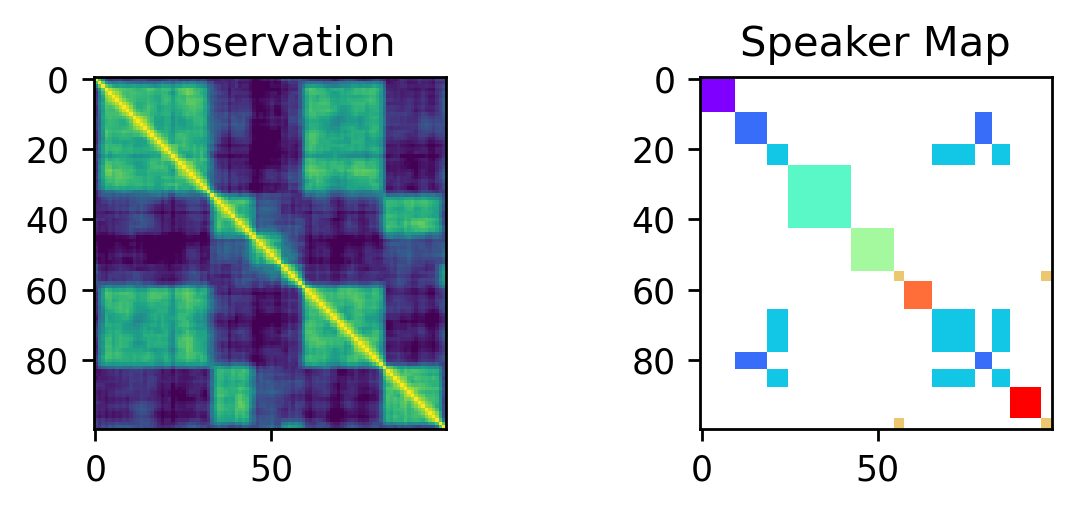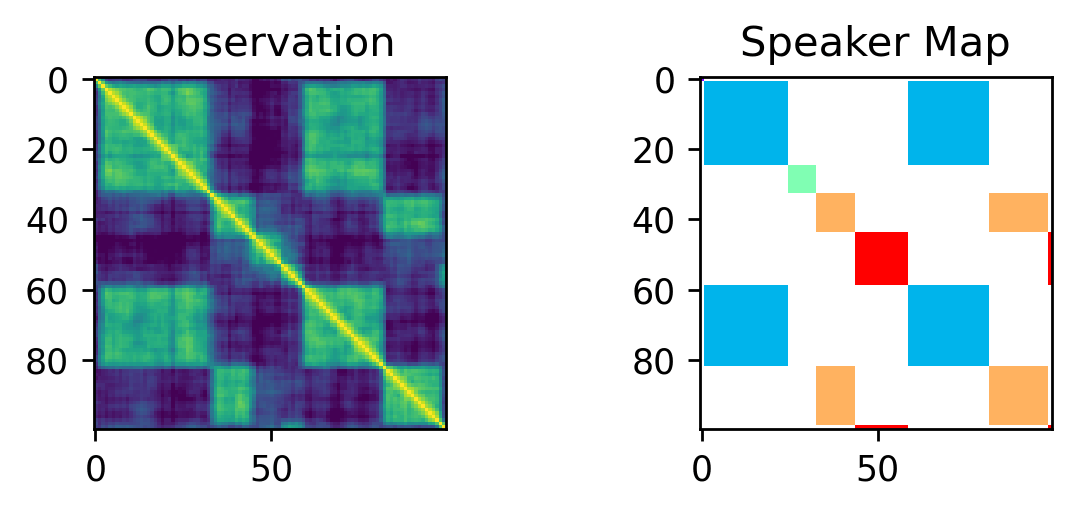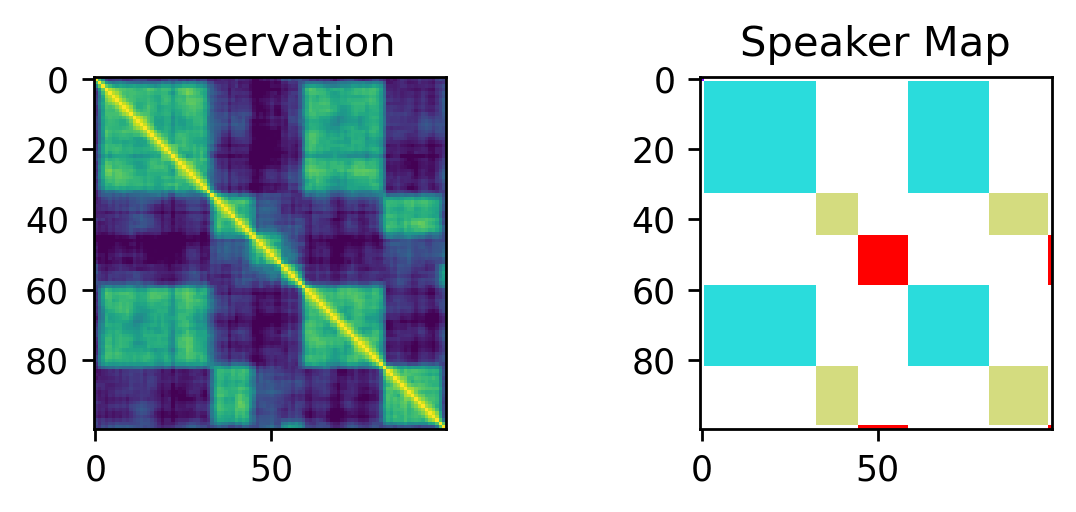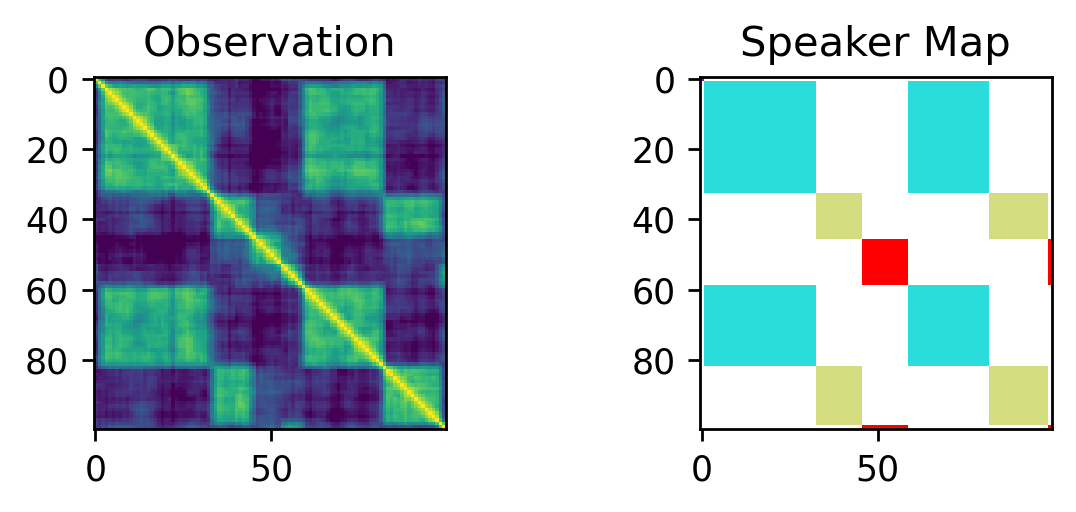
Excerpt from the notebook:
"""
matrix_model(M::Int "Max number of speakers",
T::Int "Size of the matrix (or length of the track)",
k::Int "Size of the observation band around diagonal",
poisson_rate::Float64 "Parameter shaping the `:num_segments` distribution")
Speaker similarity-matrix model.
"""
@gen function matrix_model(M::Int, T::Int, k::Int, poisson_rate::Float64)
#
# Sampling the number of segments `N` and
# their lengths `ls`, and computing
# their enpoints `ps`
#
N = {:num_segments} ~ poisson_plus_one(poisson_rate)
ls = {:len_segments} ~ dirichlet(N, 2.0)
ps = cumsum(ls)
ps[end] = 1.0 # Correct numeric issue: `ps[end]` might be 0.999999
#
# Sampling speaker ids for each segment
#
ids = [{(:id, i)} ~ categorical(ones(M)./M) for i=1:N]
#
# Mapping speaker ids to
# individual ticks.
#
xs = collect(0:1/(T-1):1)
I = [findfirst(p -> p >= x , ps) for x in xs]
ys = ids[I]
#
# Sampling entries for the similarity matrix. We distinguish
# 3 different cases:
# - Diagonal entries
# - Same speaker
# - Different speaker
#
# TODO: One could extend this by varying the values based on
# speaker similarity
#
D = zeros(T,T)
for i in 1:T, j in max(i-k,1):min(i+k,T)
if i == j
# The voice embeddings are normalized so on the
# diagonal the entries are 1.
# TODO: Don't need a random choice here really ...
D[i,j] = {:D => (i, j)} ~ normal(1, sqrt(0.001))
else
# Off-diagonal entries ramp down
# from 0.9 towards 0.5
off = 6
r = 1 - min(abs(i-j), off)/off
r = r^2
if ys[i] == ys[j]
D[i,j] = {:D => (i, j)} ~ normal(r*0.8 + (1-r)*0.5, sqrt(0.01))
else
D[i,j] = {:D => (i, j)} ~ normal(0.15, sqrt(0.007))
end
end
end
return Dict(
:T => T,
:N => N,
:ids => ids,
:xs => xs,
:ys => ys,
:D => D,
:ps => ps,
:ls => ls)
end;